平面図形 公式集 a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積 高校数学公式集 オンライン教科書 数学まるかじり 受験生に捧ぐ 標識の唄 数式の唄 ホーム 高校数学公式集 高校数学公式集 各分野で用いる必要最小限の公式を網羅しました。日頃の確認用としてご利用ください。 数学Ⅰ 数学Ⅱ 数学Ⅲ 数と式 式と証明・高次 図形の性質 内角の二等分線と比 高校数学数2の公式一覧とその証明まとめ! 4268 views 高校数学数1の公式一覧とその証明まとめ! 4192 views 高校数学数3の公式一覧とその証明まとめ! 2938 views 高校数学数Aの公式一覧とその
U9j580gf8iba369ji2w Xyz P 296
数学 図形 面積 公式
数学 図形 面積 公式-台形の高さ・面積 (4辺の長さから) 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 ひし形の面積 平行四辺形の面積 (底辺と高さから) この記事ではこんなことを書いています 数ある数学の公式の中で、面白く、そして美しい公式を紹介します。 面白い数学公式①:オイラー積の公式 オイラー積の公式 \begin{align} \sum_n \frac{1}{n^s} & = \prod_p \frac{1}{1\frac{1}{p^s}} \\ \\ n & = 1, 2, 3, \cdots \\ p & = 2, 3, 5, 7, 11, 13, 17, \cdots \\ s & = \text{\(2\)以上の



数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師
「図形の形」と「日本語」で しっかり確認しましょう。 アルファベットにするのは その後でも間に合います。 数学のテストで、 「公式を書きなさい」という問題が 出る事はほぼ無いですし、 テストに出るのは、具体的な図形の 面積を求める問題ですよね。初等数学公式集 出典 フリー教科書『ウィキブックス(Wikibooks)』 ナビゲーションに移動 検索に移動 "公式とは、数式で表される定理のことである" (出典フリー百科事典『ウィキペディア(Wikipedia)』 公式) 以下に、日本の数学教育において大学入学程度の水準までに用いられる、主公式, 重心, 外心, 内心, 垂心, メネラウスの定理, チェバの定理, 方べきの定理, 公式一覧, 平面図形, 角の二等分線と辺の比, 『教科書 数学A』 東京書籍
公式集(数学Ⅱ・B) 頭に入っていますか? <図形と方程式> ① 2点間の距離 = = A x y B x y 1 1 2 2 ( , ) ( , ) のとき 2 1 2 2 1 2 数学Ⅱの範囲の公式の一覧です。 「図書館で数学の勉強しようと思ったのに公式忘れて勉強にならない!」 という方が確認する目的に、シンプルに式だけ書いています。 いずれ理由は抜きにして使い方だけは補足するかもしれません。 中学数学では「球の体積の公式」が使える理由がわからない。 完全に理解するためには「積分」という知識を使わなきゃいけないんだ。 だからこそ、中学生の間は、 さんしろう、美味しいパイを持ってある日参上 という語呂で「球の体積の公式(3分の4 × 円周率 × 半径の三乗)」をおぼ
S S は, S = ( s − a) ( s − b) ( s − c) ( s − d) − a b c d cos 2 ( θ 2) S=\sqrt { (sa) (sb) (sc) (sd)abcd\cos^2 (\frac {\theta} {2})} S = (s− a)(s− b)(s− c)(s −d)−abcdcos2(2θ ) ただし, s = a b c d 2 s=\dfrac {abcd} {2} s = 2a b c d このページでは、 数学Aの「図形の性質の公式」を一覧にしました。 図形の性質に出てくる公式と覚え方を、わかりやすくまとめてあります。 問題集を解く際の参考にしてください! 「数学なんて何の役に立つんだよ!」 学校で習ってた頃はそう思ったものだが、いざ大人になると意外に役に立ってしまうものである。 それが中学で習った「図形」だ。 石川大樹 (いしかわだいじゅ) インターネットユーザー。電子工作でオリジナルの処刑器具を作ったり、辺境の国の変



図形問題へのアプローチ 3 怜悧玲瓏 高校数学を天空から俯瞰する




A B 2 A 2 2ab B 2 の公式は図形を使えば理解できる 数学の面白いこと 役に立つことをまとめたサイト
半角の公式を図形的に考える 現時点での図をおさらいしておきましょう。 $\mathrm{ AB=AC }=1$ で、 $\angle \mathrm{ A }=\alpha$ の二等辺三角形を考え、 BC の中点を M とし、 M から AB に下した垂線の足を P としたのでした。 このとき、 AP, BP は、それぞれ、 $\cos^2\dfrac{\alpha}{2}$, $\sin^2\dfrac{\alpha}{2}$ となる 学年 中学1年生, 単元 比例式,関数,比例,反比例,図形の移動,おうぎ形,いろいろな立体,立体の体積と表面積, キーワード 数学,関数,比例,反比例,平面図形,立体図形,球,柱,錐,りぽのーと,math 公式まとめてみました! 見にくいところもあると思いますが、見てくださってありがとうございます🌷さらに、余裕があれば、以下のヘロンの公式も知っていると良い 面積 = S s s a s b s c ( )( )( ) (sは三角形の周の半分) (5)球の体積と表面積 体積 3 3 4 = pV r , 表面積 =4pS r 2 (6)相似な図形の面積比,体積比 相似比がmnである図形の面積比は、 m n 2 2




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
角の二等分線の定理のポイントは!・内分とは内側に分けること!・外分とは外側に分けること!・内角の二等分線の定理はAB:AC = P からの 数列の単元で、苦手な人が多い問題をわかりやすく解説しました。 高校数学A図形の性質 公式一覧(チェバ・メネラウス・接弦・方べき) このページでは、数学Aの「図形の性質の公式」を一覧にしました。 図形の性質に出てくる公式と覚え方を、わかりやすくまとめてあります。 問題集を解く際の参考にしてください! 目次1 図形の 数学A中学数学空間図形 角柱・角錐(すい) 角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ここで紹介している内容は17年3月時点の情報です。ご紹介し



Q Tbn And9gcqjobggcmt23 2z3kno11yv3jyxklvrxkobpwlhwovwikso5zii Usqp Cau




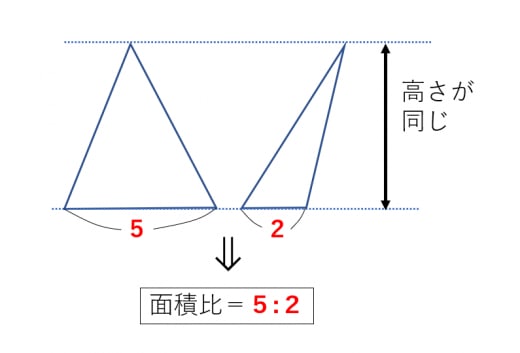
数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
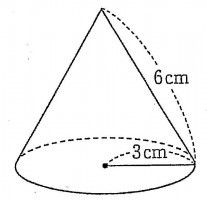
図 式 扇形 A = 面積 L = 円周の長さ R = 半径 扇形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) それでは、問題を通して球の公式をしっかりと身につけていきましょう! 半径6㎝の球の体積、表面積をそれぞれ求めなさい。 解説&答えはこちら 答え 体積: 表面積: 体積 表面積 次の図形の体積、表面積をそれぞれ求めなさい。 解説&答えはこちら数学:公式・図形の性質・条件テスト 連立・一次関数 理科:1分野・2分野暗記テスト 記述演習 料金 \22,000(2日分) (テキスト・プリント代込み) 講習時間・回数 1コマ 3時間 × 週5日 講習内容 5科目の総復習・演習と解説 学校課題の難問解説 料金 \45,000




中1 空間図形 公式一覧 中学生 数学のノート Clear




ボード 支援教材 のピン
図形の公式 中学生 数学のノート Clear 表紙 1 公開日時 21年07月22日 15時50分 更新日時 21年07月22日 15時54分 中学生 全学年 数学 高校受験数学公式集 図形編 131 2 深雪 *数学*~平面図形 基本まとめ~ 1 12 翔虹⚡︎ 数学1年生のまとめ 118 4 こもつな 中1 数学 平面図形 111 6 yui キソカク数学 一年まとめ 110 7 ( ´・わωか กめ` ) 数学中1の公式まとめ 103 5 り ぽ 🕊𓂃𓈒𓏸 YuY の円と円錐 103 0 YuY 〈数学受験算数における図形問題の公式集 東海地区における難関中学受験者向け 0 公式一覧 (画像目次) 1 角度 の公式・考え方 2 長さ の公式・考え方 3



中学生の数学の公式一覧 図形の定理から解の公式まで学年別に分かりやすく解説 学びtimes



教科書レベルの問題一覧と解答 数学a 図形の性質 教科書より詳しい高校数学
図形で使う公式・定理の一覧 扇の孤の長さ"l" 扇の半径をr、中心角をx、孤の長さをlとしたとき 扇の面積"s" 扇の半径をr、中心角をx、面積をSとしたとき 角柱の体積"v数学Ⅰ 図形と計量 復習 復習 直角三角形と三角比 三角比を単位円で表す 90n°±θの三角比の値 (1) 三角形の面積から逆算 対角線と四角形の面積 過去問解説 大学入学共通テスト 21追試 数学ⅠA 第1問 2 21本試 数学ⅠA 第1問 2 18問題例 記述式を含む 問題例1 3 18試行調査 数学ⅠA 第2問 18 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b (三角形の面積)=(abc)×r× 1 2 12 平行線と比例 a
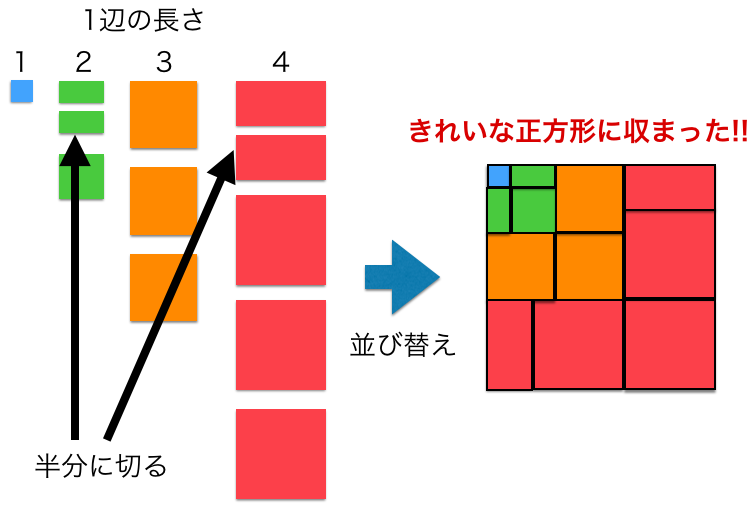



暗記しない数学 3乗和のシグマ公式を図形で理解してみる ロボット It雑食日記




高校数学 2点間の距離の公式 映像授業のtry It トライイット
高校数学の公式一覧とその証明をまとめました。 大学受験などに役立ててください。 また高校をすでに卒業した人もパズル感覚で公式の証明をするのも楽しいのでぜひチャレンジしてみてください。 高校数学まとめ ・数1まとめ 数と式、集合と論理、二次関数、図形と計量、データの分析 ・数Aまとめ 場合の数と確率、整数の性質、図形の性質 ・数2 高校数学公式集 オンライン教科書 数学まるかじり 受験生に捧ぐ 標識の唄 数式の唄 ホーム 高校数学公式集 「三角比」の公式集 「三角比」の公式集 三角比の定義 ↑答えが分かったら画像をクリック↑ 特別な角度の三角比 ↑答えが分かったら画像をクリック↑ 補角の三角比
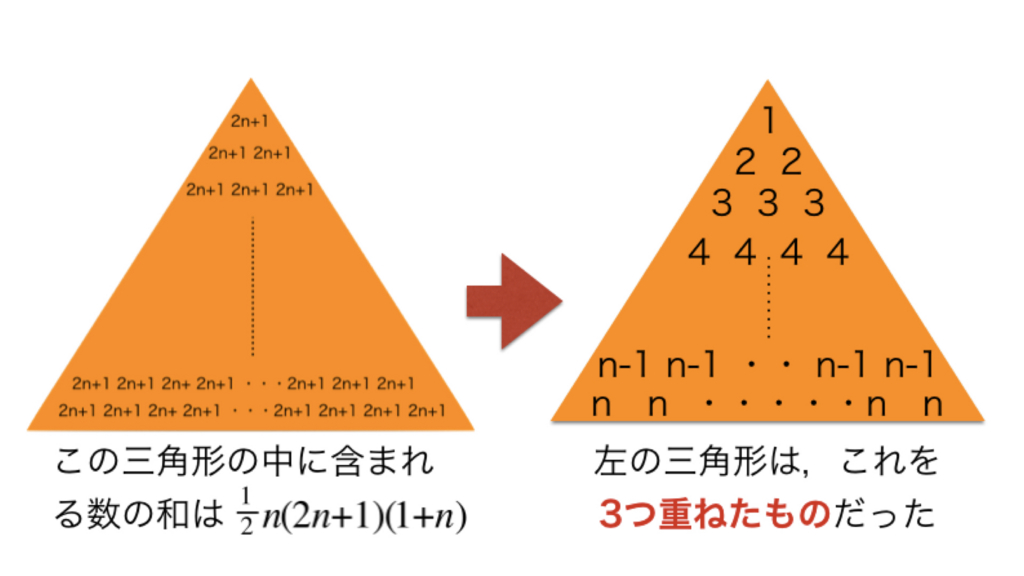



暗記しない数学 図形で理解するシグマ公式 ロボット It雑食日記
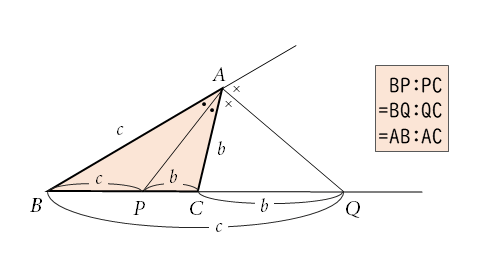



数学の公式 定理集 図形の性質 日々是鍛錬 ひびこれたんれん
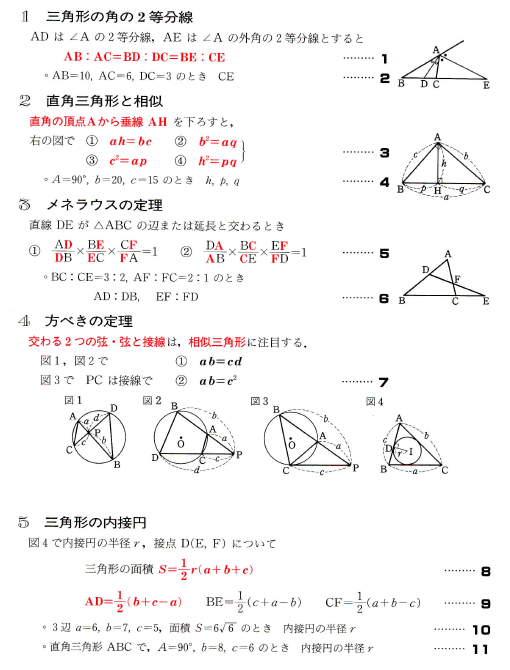



中学数学 図形 さくらの個別指導 さくら教育研究所 Skredu




高校数学復習記録 その8 桜花 現役バイト塾講師 Note




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学生の数学の公式一覧 図形の定理から解の公式まで学年別に分かりやすく解説 学びtimes




中1数学 平面図形で勉強する 図形の移動 3つのまとめ Qikeru 学びを楽しくわかりやすく
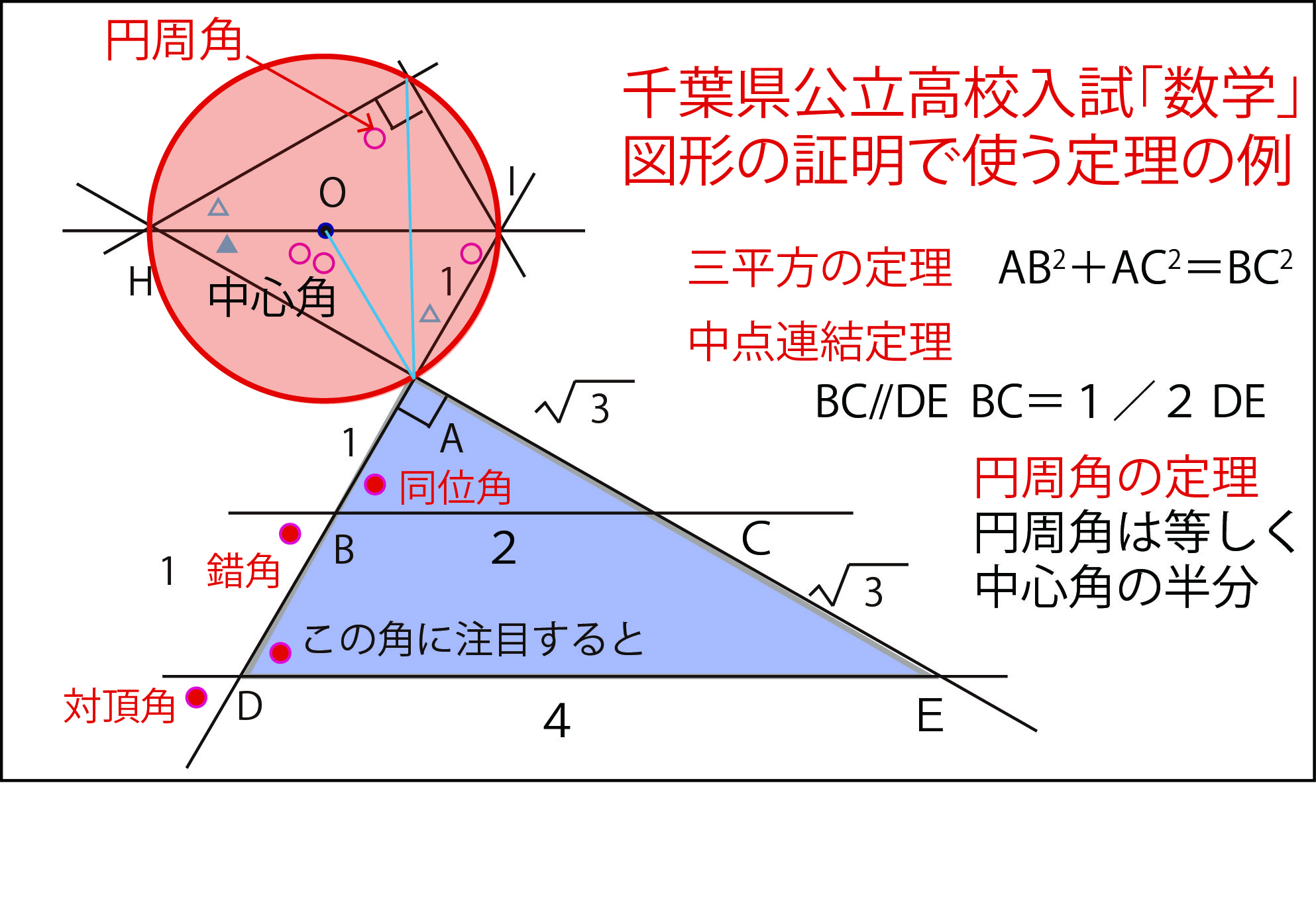



10月21日 11月18日 中教協の日 県公立高校入試 2月 数学 対策特別 講座 図形が見える のご案内 船橋市議会議員 朝倉幹晴公式サイト




中3 差がつく 裏技 高校受験のための数学の定理まとめ 中学生 数学のノート Clear
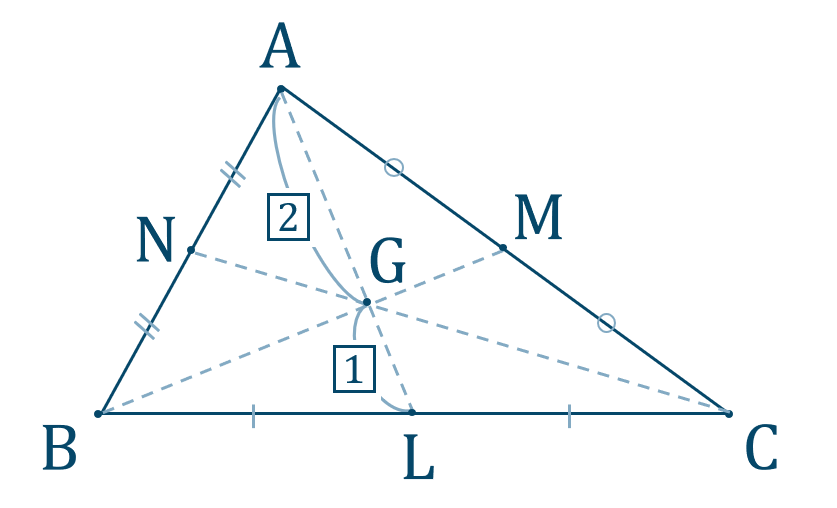



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師




高校数学 円の接線公式 映像授業のtry It トライイット
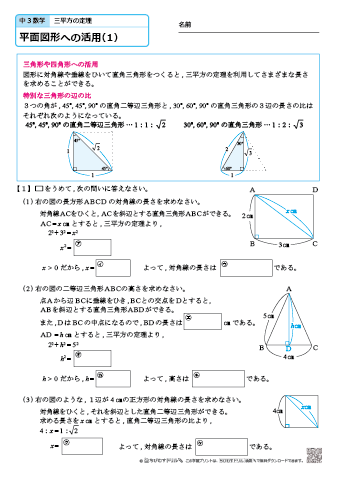



中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生



受験数学かずスクール 中学の因数分解の公式の図形的な覚え方




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




図形と方程式は2時間で解けるようになる 外資系コンサルタントが主夫になったら




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア
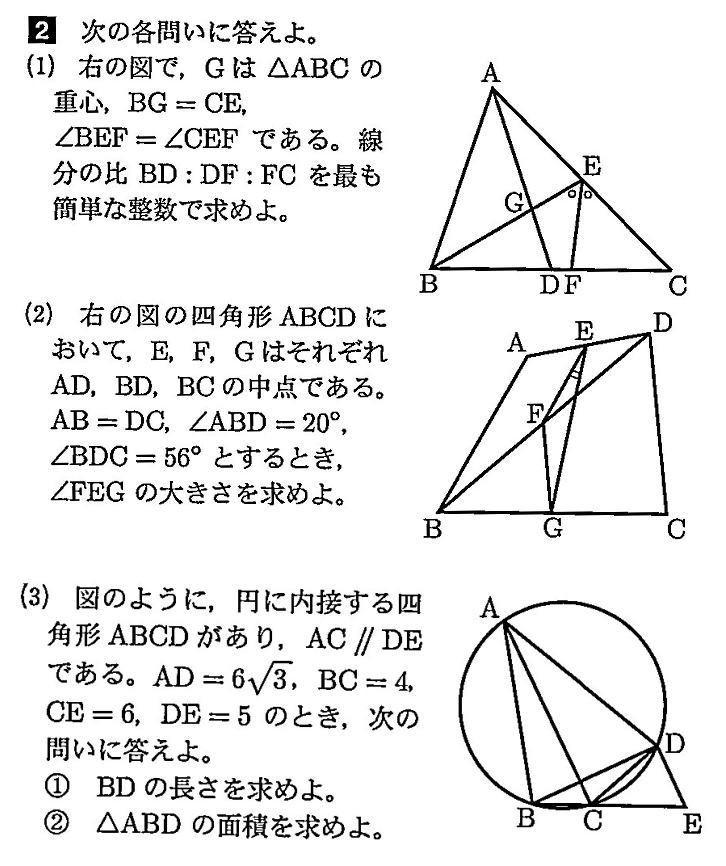



城北高校年度数学入試問題2 平面図形 中学受験から医学部受験までプロにお任せ プロ家庭教師集団スペースone 公式



1




高1 数a図形の性質 公式 高校生 数学のノート Clear



1
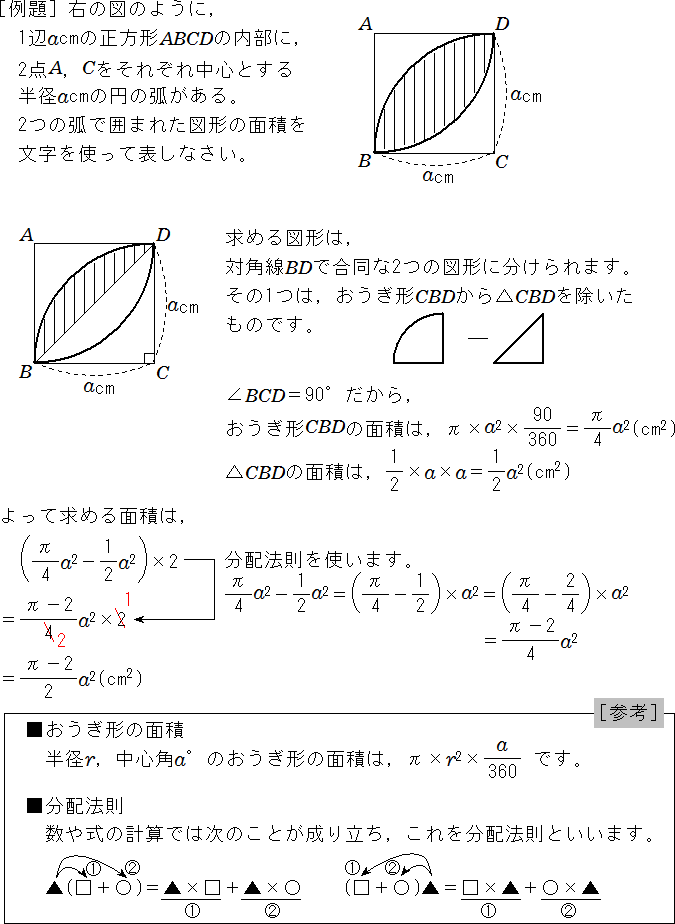



式の計算 文字を使った変わった図形の面積の求め方 中学数学 定期テスト対策サイト




中1 数学 中1 立体の表面積 Youtube




球の表面積と体積の公式 数学fun




数探高校講座 数学 図形と計量 27 空間図形の軽量 数学探究所




高校数学 座標平面上の三角形の面積の公式 受験の月




相似な図形 補助線を引いて考える相似の問題 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




中1 中1数学 空間図形 体積と表面積の公式一覧 中学生 数学のノート Clear
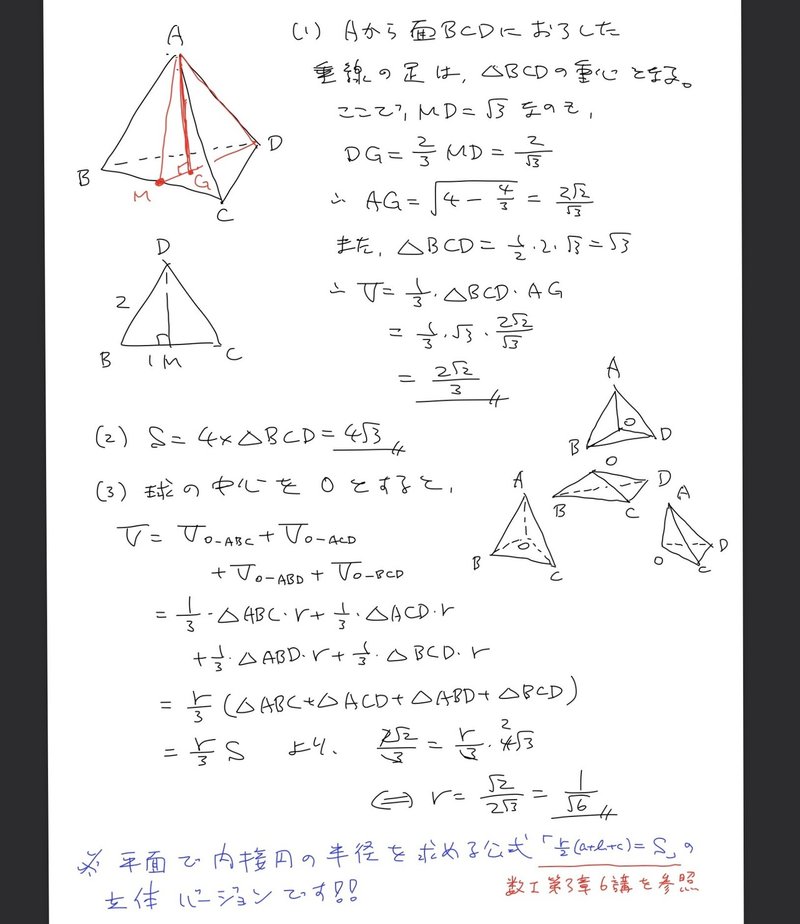



高校数学無料問題集 数a 第2章 図形の性質 空間図形 桝 ます Note
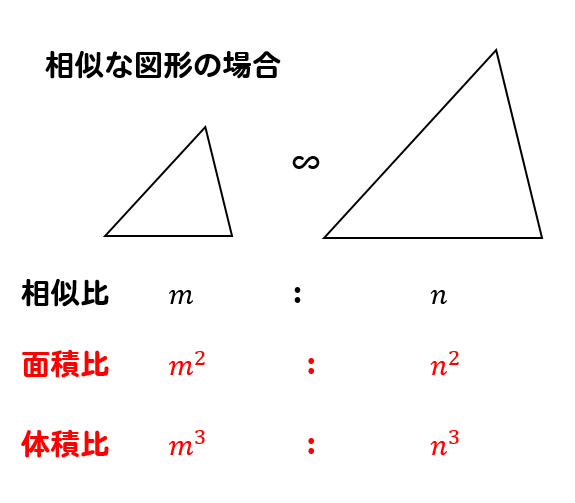



中学数学 高校入試で使える重要公式を一覧でまとめておくよ 数スタ




高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月
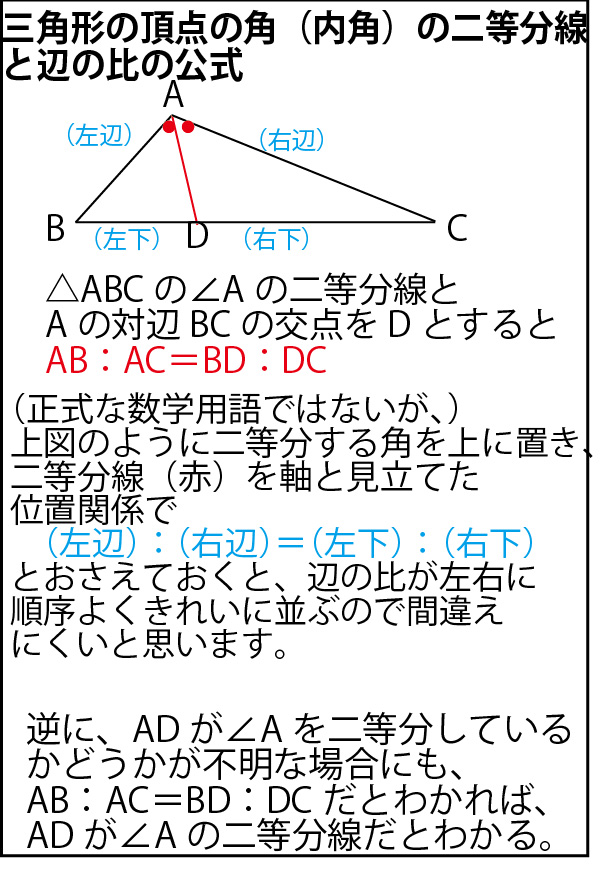



18年大学入試センター数学ia第5問 図形 選択問題 配点点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




世界一わかりやすい数学問題集中1 6章 空間図形
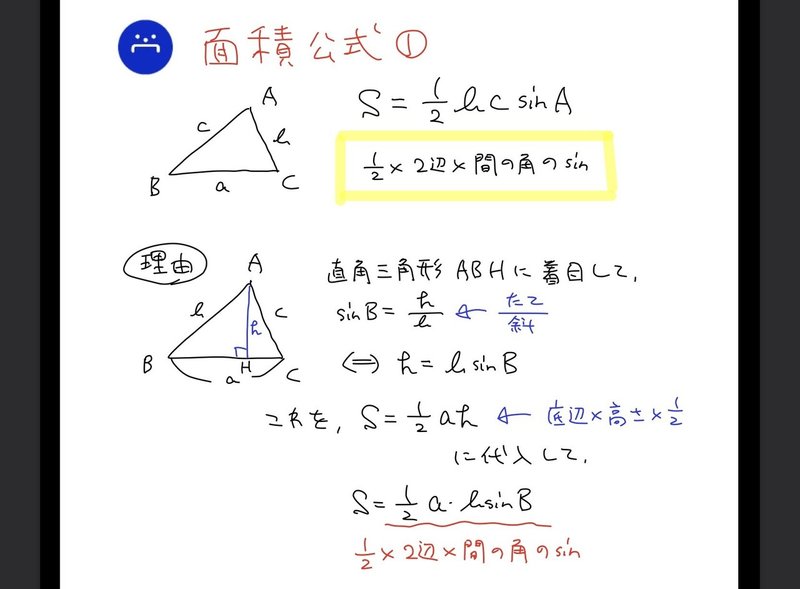



高校数学無料問題集 数 第3章 図形と計量 面積 桝 ます Note
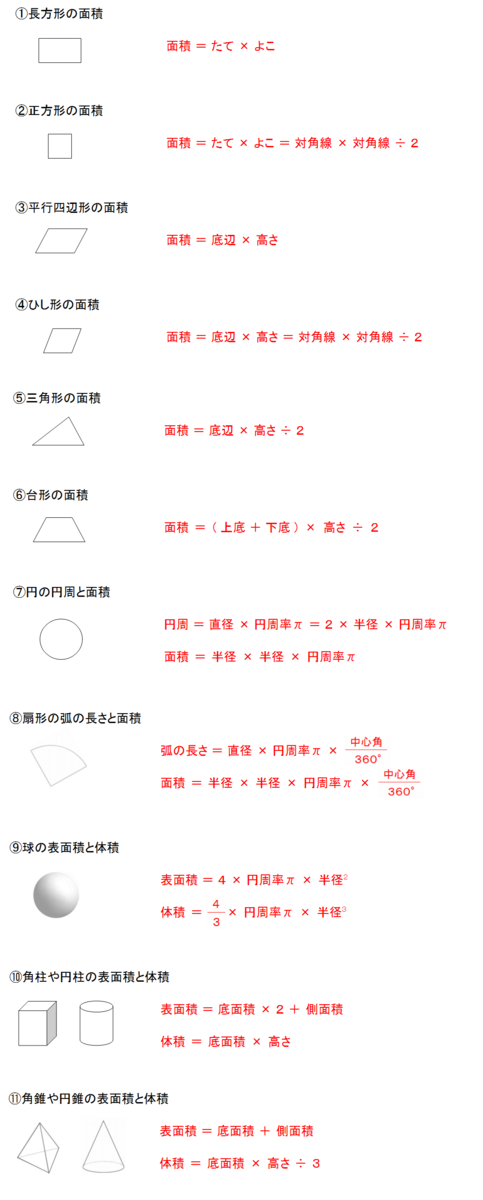



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
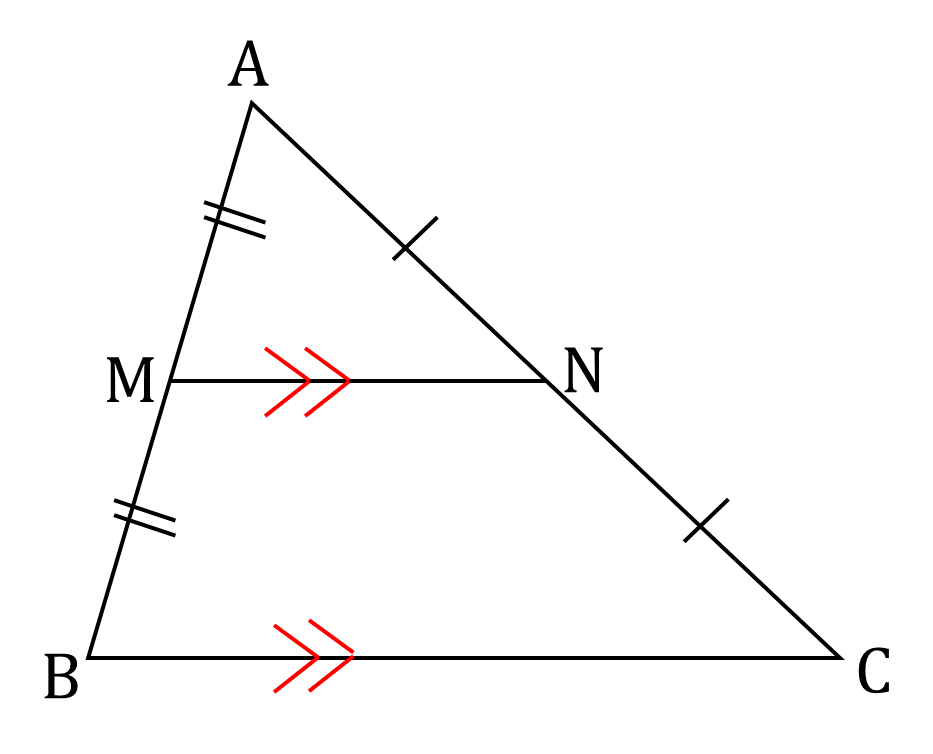



初心者必見 絶対に必要な重要中学数学の10の公式まとめ



芋づる式で覚える空間図形の公式一覧 中学1年数学 空間図形
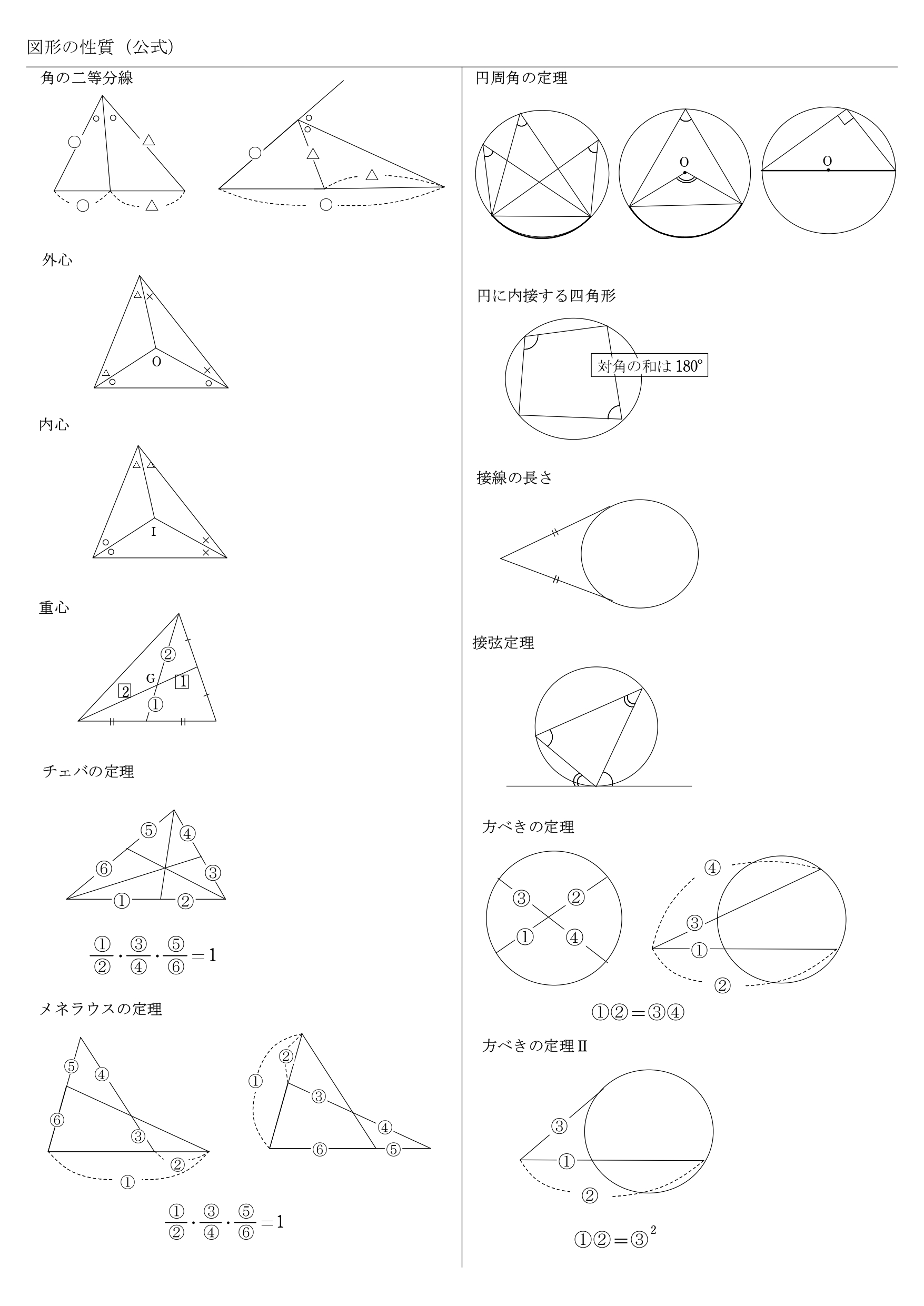



高校数学a 図形の性質 公式一覧 チェバ メネラウス 接弦 方べき 学校よりわかりやすいサイト
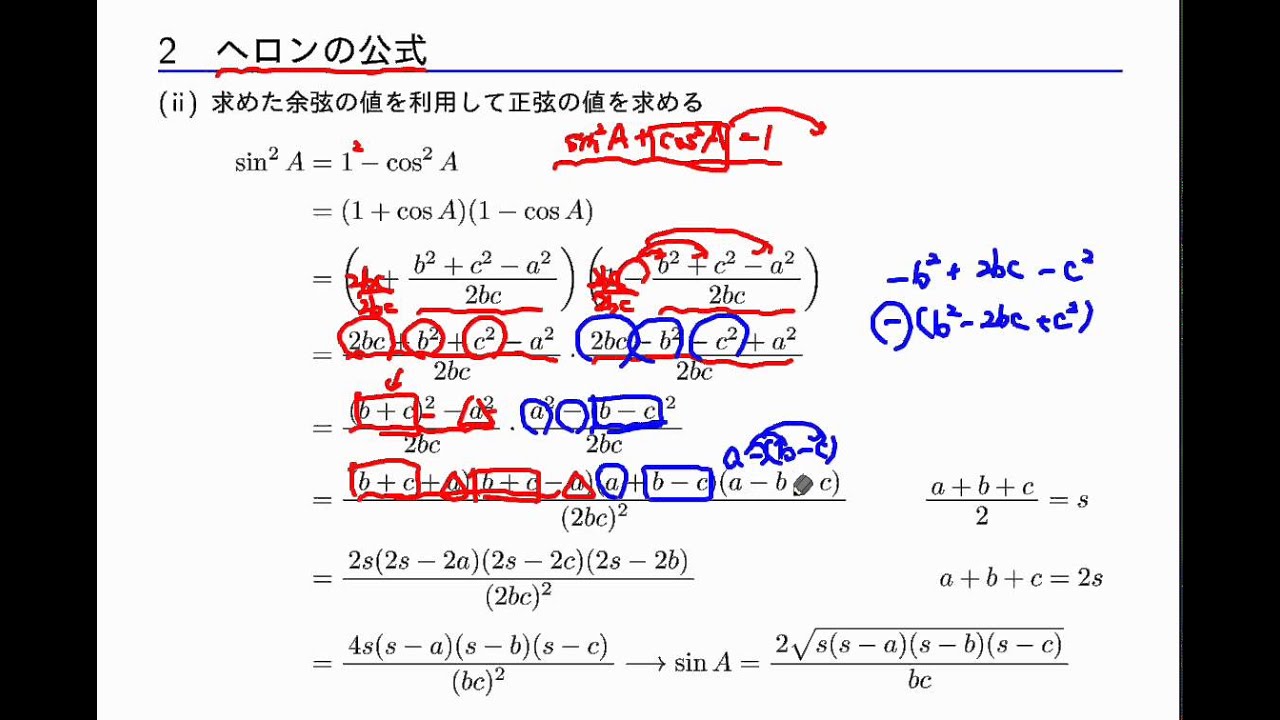



数学i 図形の計量 2 2 ヘロンの公式 Youtube
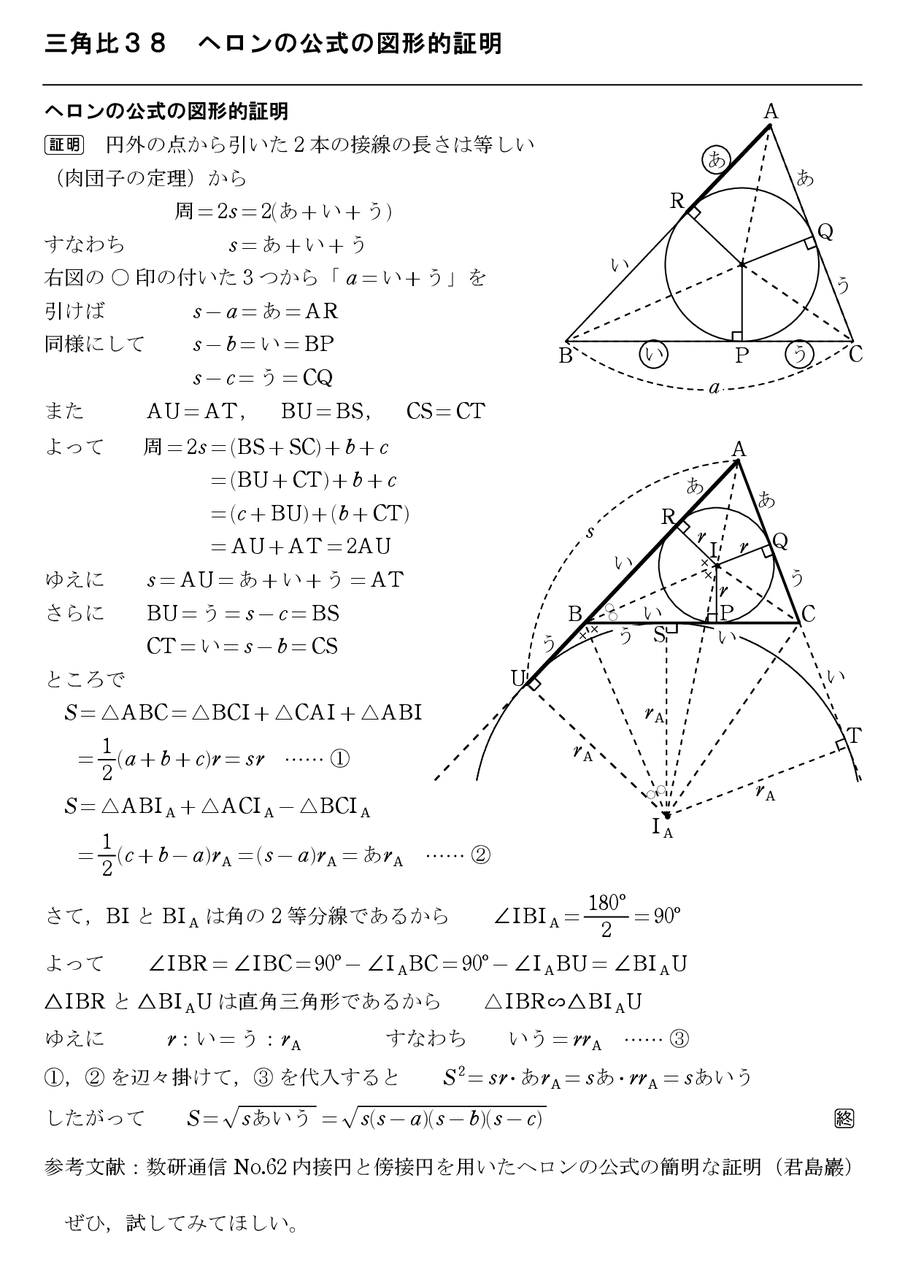



三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する




数学a基礎 図形の性質 演習コース 数学a基礎 演習コース 石井大裕 数学 Kindleストア Amazon



U9j580gf8iba369ji2w Xyz P 296




図形と方程式は2時間で解けるようになる 外資系コンサルタントが主夫になったら




高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月



図形と計量の問題 Of 京極一樹の数学塾会員頁
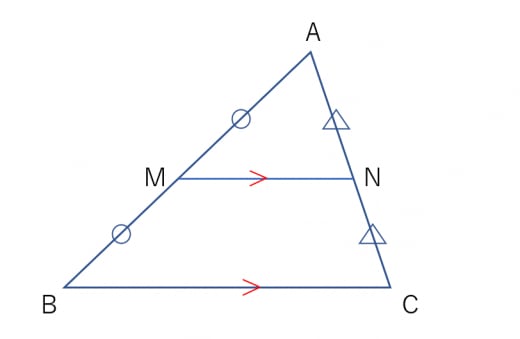



中学生の数学の公式一覧 図形の定理から解の公式まで学年別に分かりやすく解説 学びtimes
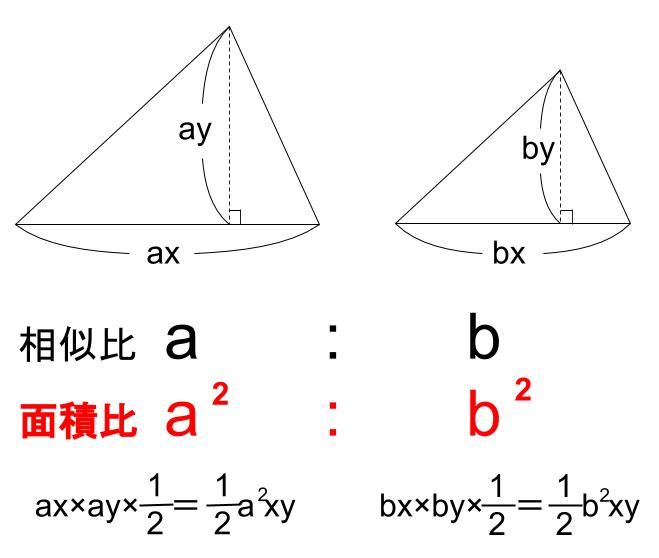



中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
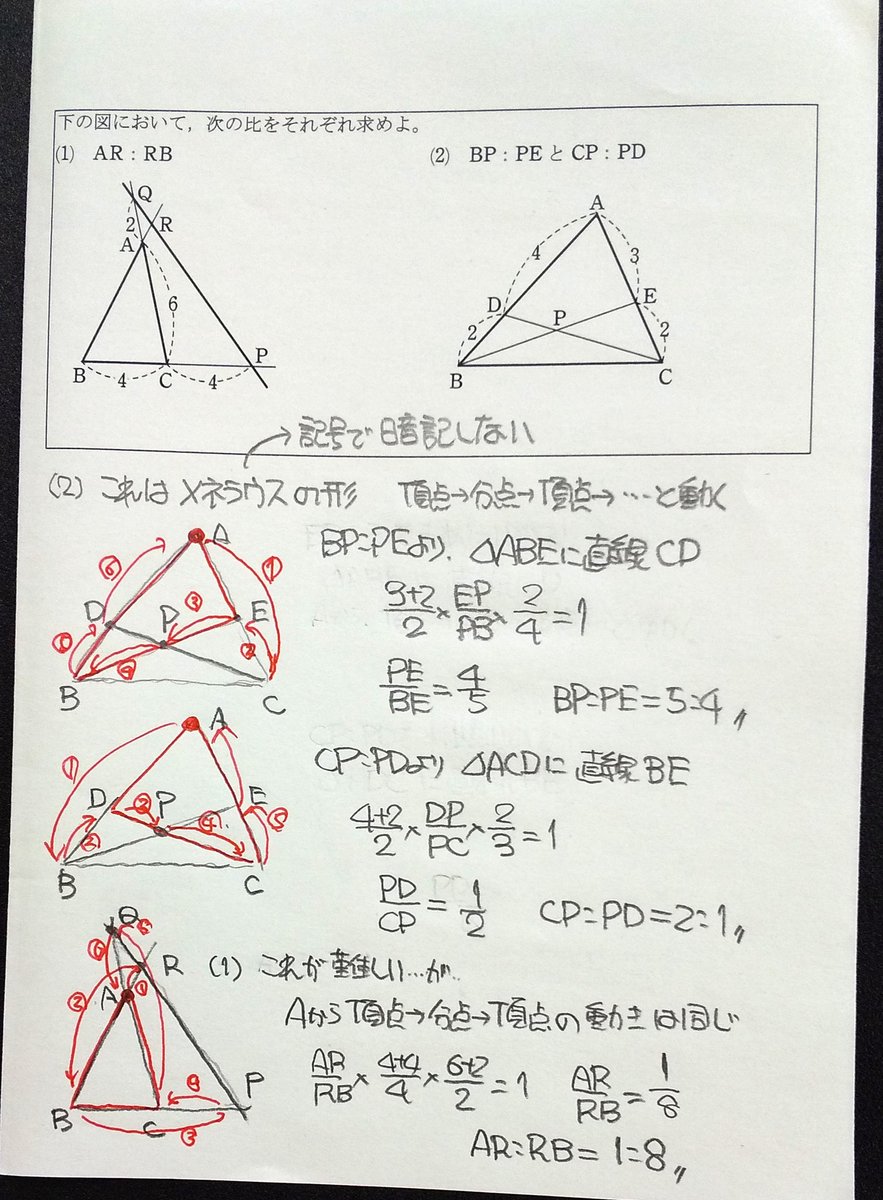



原田 浩明 בטוויטר Sサクシード063 チェバの定理 メネラウスの定理 公式を文字で暗記しないで 形と動きで使えるようにする 複雑な図形 の中に公式が使える形を見つける能力が必要 高校 数学 1年 数学a 図形の性質 チェバ メネラウス




Amazon Co Jp お風呂学習ポスター 受験教材 数学公式一覧表 おもちゃ
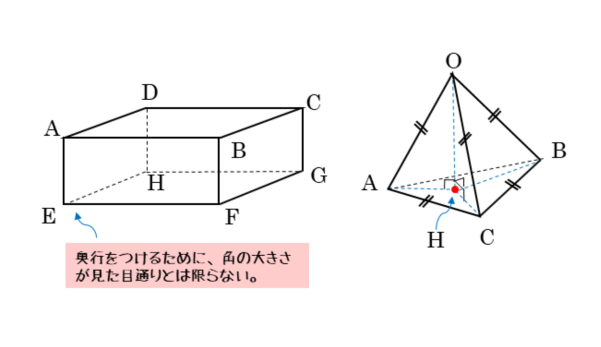



図形と計量 空間図形への応用について 日々是鍛錬 ひびこれたんれん
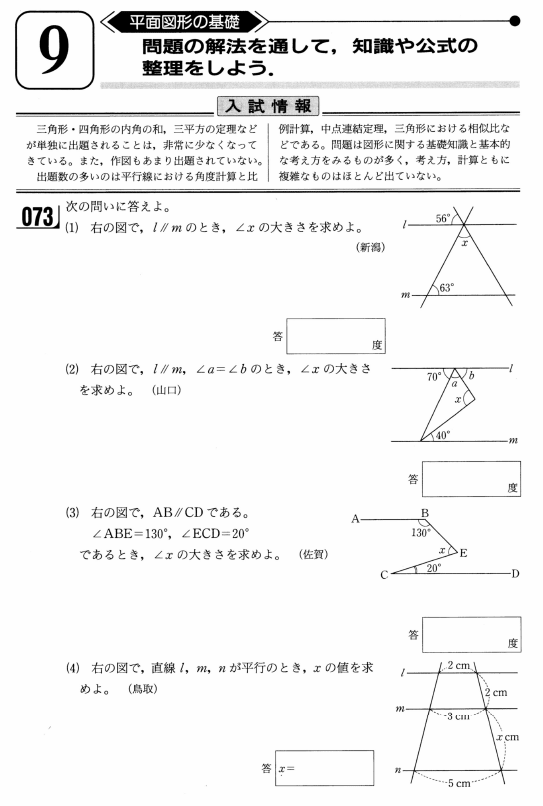



平面図形の基礎 英語 数学 さくら教育研究所 中学 高校受験 Skredu



算数 テーマ別 ポイント集 立体図形 1 10 中学受験の勉強法 偏差値アップの学習法
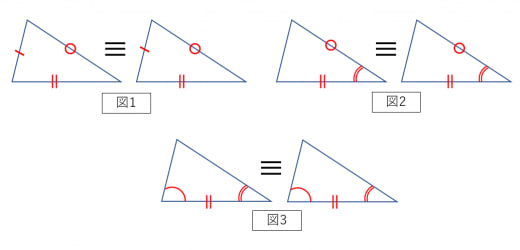



中学生の数学の公式一覧 図形の定理から解の公式まで学年別に分かりやすく解説 学びtimes
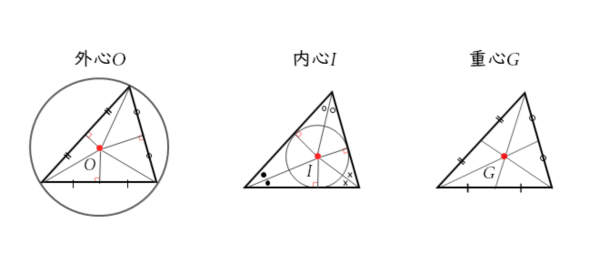



数学の公式 定理集 図形の性質 日々是鍛錬 ひびこれたんれん
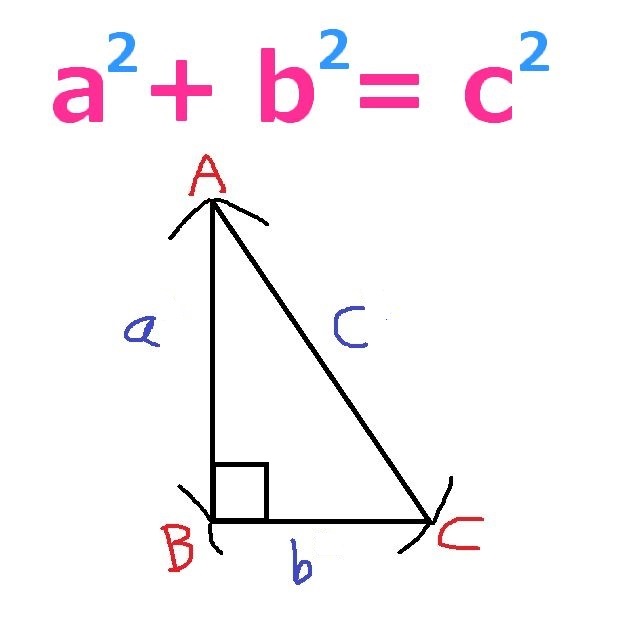



図形問題は地図と歴史を見よ 数学弱者の救済数学 2 連載jp




図形と計量 三角比 頻出図形問題 凝縮一目瞭然チャートを公開 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
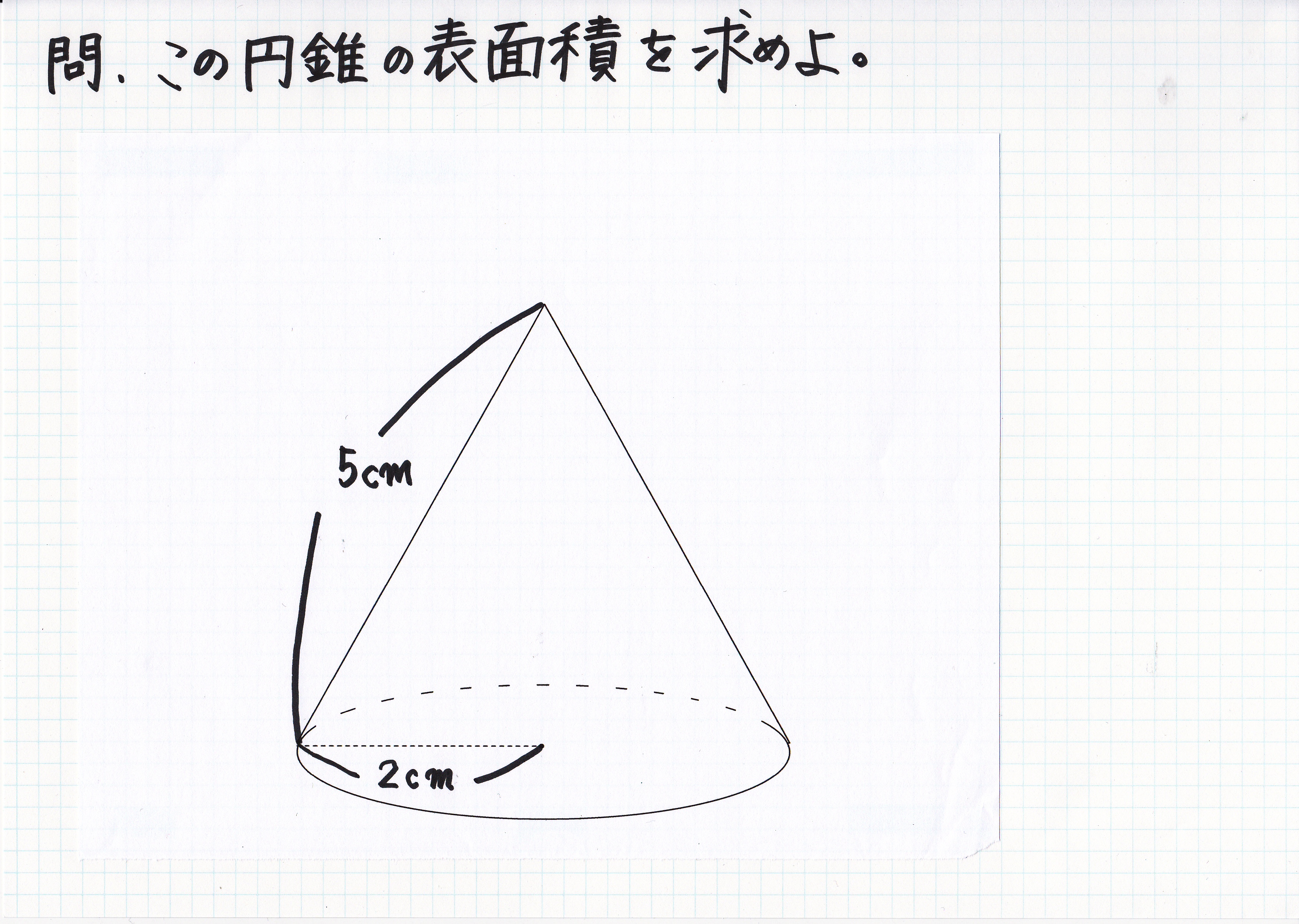



円錐の空間図形から表面積を求める基本公式と裏技 現役塾講師のわかりやすい中学数学の解き方



図形公式 大学受験の王道




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



中学数学図形問題 おうぎ形と直角三角形を一回転させた表面 Yahoo 知恵袋




オリジナル教材 おいしい数学
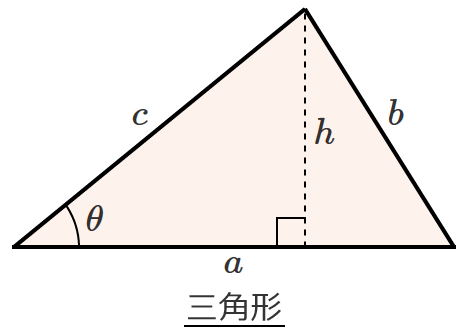



電気数学のお勉強 図形
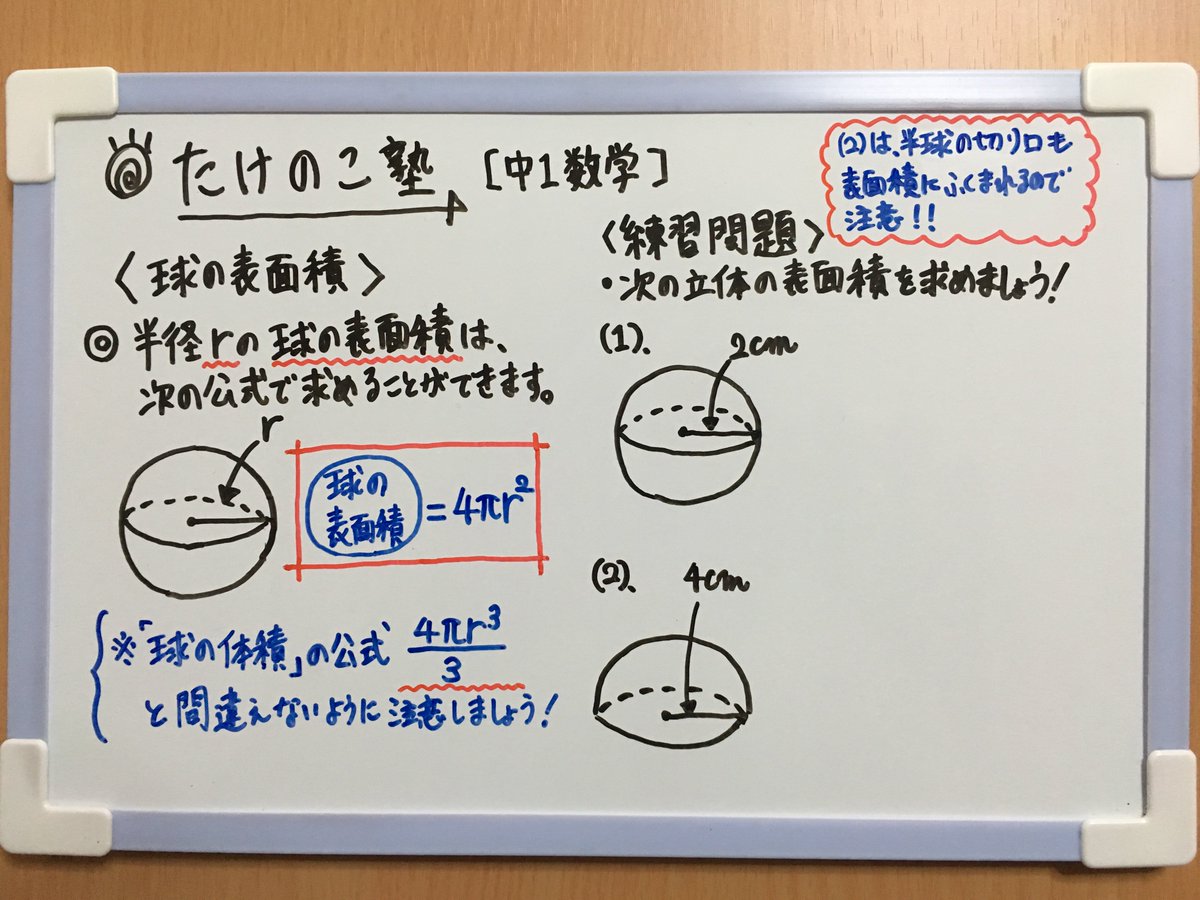



たけのこ塾 中1数学 今回は 空間図形 球の表面積 についての問題です 球の体積の公式 と間違えないように気を付けましょう 詳しくはアップしている画像をご覧下さい 勉強垢 中1 数学 空間図形 Youtube




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




難関高校合格のための中学数学公式一覧 10秒で解けますか




高校数学 放物線と直線で囲まれる図形の面積 映像授業のtry It トライイット



中学数学単元別 図形と計量の組み合わせ 数学 中学校 教材 問題集 307 学林舎 通販 Yahoo ショッピング




中学数学の図形で使う公式 定理の一覧 中学数学 By となりがトトロ マナペディア



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



円 に関するチャートを作ってみました 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
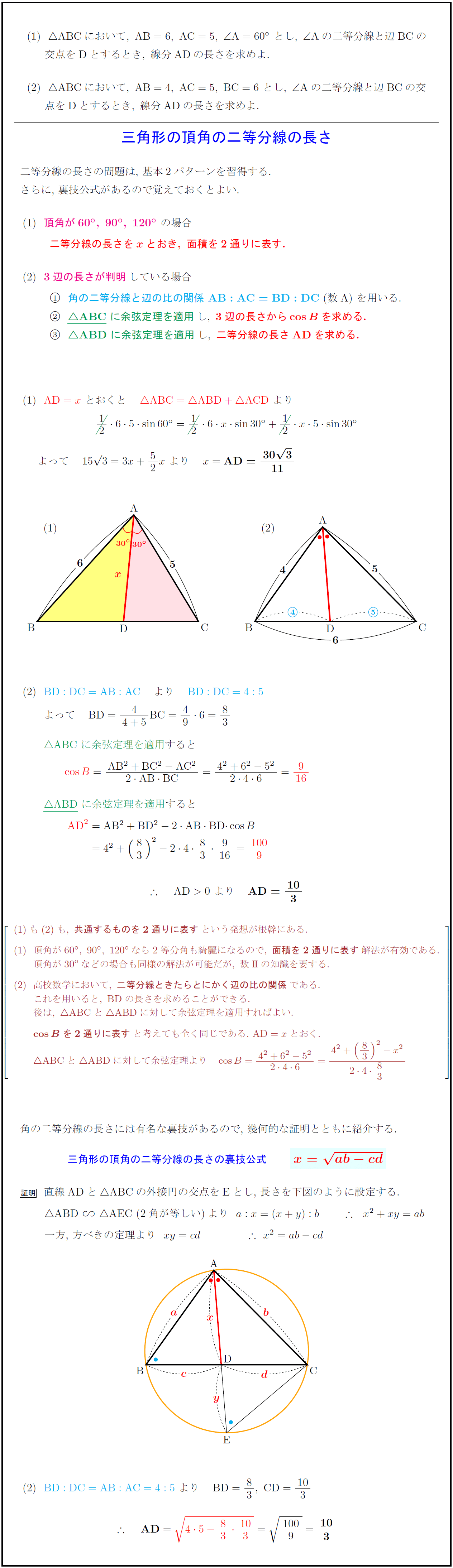



高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月




これで分かる 平面図形 中学生 数学のノート Clear
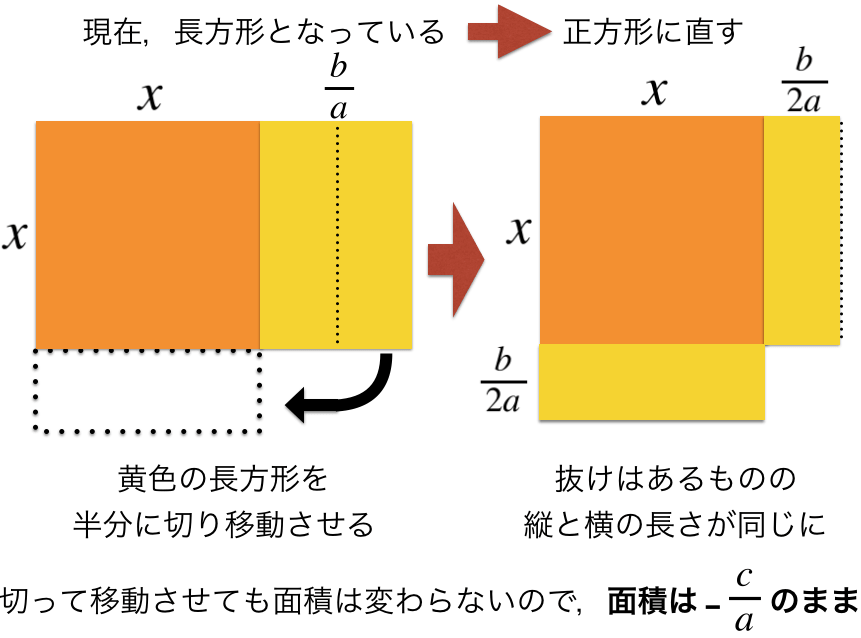



中学数学で一番複雑な公式 解の公式 を図形的に捉えてみる ロボット It雑食日記




数学1 解の公式 図形的な意味 Youtube




数探高校講座 数学 図形と計量 19 三角比 数学探究所




お風呂学習ポスター 受験教材 数学公式一覧表 大 60 42cm Acreditta




高校数学 線分abを m nに内分する点p 映像授業のtry It トライイット



塾長の備忘録 図形と方程式公式まとめ




高校数学 三角形の重心公式 映像授業のtry It トライイット




中学数学の図形で使う公式 定理の一覧 中学数学 By となりがトトロ マナペディア




空間図形



1




高校数学テクニック集 002 数学 A 三角比 四角形の面積を求める公式 大学受験対策 数学i 図形と計量 学習塾 Dear Hope ディアホープ 改訂 Youtube




高1 数1 図形と計量 公式 高校生 数学のノート Clear




角錐 円錐の体積と表面積の公式 数学fun




高校数学 図形と方程式 教科書 問題 解答 公式 解説 学校よりわかりやすいサイト




中1 中1数学 空間図形公式まとめ 中学生 数学のノート Clear




中学 高校で習う三角形の面積公式 Memory Map 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



平面図形 高校数学の美しい物語




数学公式の語呂合わせ 数式は楽しく覚えよう 数学の面白いこと 役に立つことをまとめたサイト
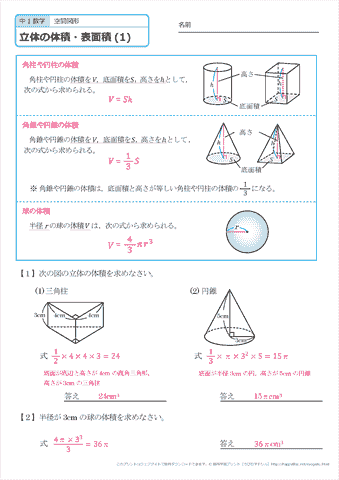



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生


