You can put this solution on YOUR website!Y = 2x 4 y = 2 x 4 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the form y = m x b y = m x b m = 2 m = 2Simple and best practice solution for y=2(x3)(x4) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so

Misc 2 Verify Given Function Is A Solution Of Differential
(x-2)(y+2x-4)= x-2 ^3 y=x+a
(x-2)(y+2x-4)= x-2 ^3 y=x+a-Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyMaximize 5 3x 4y x^2 x y y^2 WolframAlpha Have a question about using WolframAlpha?




1 Functions
Solution for y = 2x 4 y = x 2 Plot two lines by clicking the graph Click a line to delete it 10 8 7 5 4 10 9 8 3432 10 3 The derivative of x − 2 is 1 y'(x) = 3(x2 9)4(x −2)2 (x − 2)3 d dx (x2 9)4 Now we use the chain rule on the second term d dx (x2 9)4 = d du u4 du dx where u = x2 9 d du u4 = 4u3 y'(x) = 3(x2 9)4(x −2)2 (x − 2)24(x2 9)3X − 2 = 0 x 2 = 0 Add 2 2 to both sides of the equation x = 2 x = 2 x = 2 x = 2 Set x 1 x 1 equal to 0 0 and solve for x x Tap for more steps Set the factor equal to 0 0 x 1 = 0 x 1 = 0 Subtract 1 1 from both sides of the equation
8x2y2/4x3y3 Final result 2x5y5 Step by step solution Step 1 y2 Simplify —— 4 Equation at the end of step 1 y2 (((8 • (x2)) • ——) • x3) • y3 4 Step 2 Equation at the end of step 2 y2Which phrase best describes the translation from the graph y = (x 2)2 to the graph of y = x2 3?Divide 2, the coefficient of the x term, by 2 to get 1 Then add the square of 1 to both sides of the equation This step makes the left hand side of the equation a perfect square x^ {2}2x1=y41 Square 1 x^ {2}2x1=y3 Add y4 to 1 \left (x1\right)^ {2}=y3 Factor x^ {2}2x1
X^45x^24=0 \sqrt{x1}x=7 \left3x1\right=4 \log _2(x1)=\log _3(27) 3^x=9^{x5} equationcalculator y=2x4 en Related Symbolab blog posts High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 bx c = 0, where a, b, and c2 units left and 3 units up 2 units left and 3 units down 2 units right and 3 units up 2 units right and 3 units down C What is the first step when rewriting y = 4x2 2x 7 in the form y = a (xRewrite the expression Multiply − 1 1 by 1 1 Subtract 1 1 from 4 4 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k,



1




Worked Example Implicit Differentiation Video Khan Academy
Two parabolas are the graphs of the equations y=2x^210x10 and y=x^24x6 give all points where they intersect list the points in order of increasing xcoordinate, separated by semicolonsGraph a function by translating the parent function Explanation Another way of finding the axis and vertex is to complete the square y = x2 − 4x 3 y = (x − 2)2 −1 for the vertex find the x value that makes the bracket = 0 x = 2 ⇒ y = −1 vertex (2, − 1) axis of symmetry simply the the xvalue above X = 2 with the graph as before




If X 3 2x 2y 2 5x Y 5 0 And Y 1 1 Then A Y Prime 1 4



Math Scene Derivatives Lesson 2 Differentiating Polynomials
The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2xy3=0 x 2 − 2 x − y − 3 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and 3y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} 求微分方程y'+x=√(x^2+y)的通解 42 y=2/x3/x^3的导数 需要解题过程谢谢,知道怎么计算但是算不出来,就是计算过程出问Simple and best practice solution for y=x^34x^23x2 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework



2



Graphing Types Of Functions
First type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer is right More ExamplesA Stepbystep explanation Given the 2 equations y = 2x 4 → (1) y = x² x 2 → (2) Substitute y = x² x 2 into (1) x² x 2 = 2x 4 (subtract 2x 4 from both sides) x² x 6 = 0 ← in standard form (x 3) (x 2) = 0 ← in factored formPre Calculus Equations Inequalities Simultaneous Equations System of Inequalities Polynomials Rationales Coordinate Geometry Complex Numbers Polar/Cartesian Functions Arithmetic & Comp Conic Sections Trigonometry Calculus




9 For F X 2x2 X 7 And G X X 1 Find F Chegg Com




Solved Solve For X In Terms Of Y Y 2x 4 X 3 A X 4 Chegg Com
Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with 0 0 in the expression f ( 0) = − ( 0) 2 2 ( 0) − 4 f ( 0) = ( 0) 2 2 ( 0) 4 Simplify the result Find an answer to your question Solve the system of equations y=2x4 y=x^2x2 jle1042 jle1042 Mathematics High School answered Solve the system of equations y=2x4 y=x^2x2 2 See answers MrGumby MrGumby Answer The two intersections would be (3Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method y=2x4;3y=x2 Tiger Algebra Solver




Implicit Differentiation



1
For example, the polynomial x 2 y 2 3x 3 4y has degree 4, the same degree as the term x 2 y 2 However, a polynomial in variables x and y , is a polynomial in x with coefficients which are polynomials in y , and also a polynomial in y with coefficients which are polynomials in xX2 = 0 Approaching (0;0) along the yaxis (x = 0), lim (x;y) !(0;0) 2xy x2 2y2 = lim y 0 0 2y2 = 0 Approaching (0;0) along the line y = x, lim (x;y)!(0;0) 2xy x2 2y2 = lim x!0 2x2 3x2 = 2 3 The limit does not exist Example Find the limit lim (x;y)!(0;0) x2y x4 y2 if it exists Approaching (0;0) along the line y = mx, lim (x;y)!(0;051 Find the Vertex of y = x 2 2x1 Parabolas have a highest or a lowest point called the Vertex Our parabola opens up and accordingly has a lowest point (AKA absolute minimum) We know this even before plotting "y" because the coefficient of the first term, 1 , is positive (greater than zero) Each parabola has a vertical line of symmetry




Slope From Equation Video Khan Academy




Edexcel Core Mathematics C1 May 17
PLAY Match Gravity Which ordered pairs are in the solution set of the system of linear inequalities?Y=x3 y=x^22x4 A x3=x^2 B x3=x^22x4 C y=(x3)^22(x3) dragonpikachucharman dragonpikachucharman Mathematics College answered To solve x 2 3x – 4 = 0 subtract x 2 3x – 4 = 0 from y = x 2 3x – 4, The points of intersection of the parabola with the x axis are the points (4, 0) and (1, 0), whose x – coordinates (4, 1) is the solution, set for the equation x 2 3x – 4 = 0



Math Scene Equations Iii Lesson 2 Quadratic Equations




Answered Let ƒ X Y 2x 3y 4 Find The Bartleby
Find an answer to your question what is the result of substituting for y in the bottom equation?Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 2x4=y 2 x 4 = y Subtract 4 from both sides Subtract 4 from both sides 2x=y4 2 x = y − 4 Divide both sides by 2Y >1/2 x y




Sat Ii Math Level 2 Test 05 Solution 1 If 8x 12 K 3 2x 3 For All X Then K A 1 4 B 3 C 4 D 12 E 24 8x 12 K 3 2x 3 Ppt Download




How To Draw Y 2 X 2
Volume of the region bounded by y=x^24,y=2xx^2, y=0 rotated around y=2,2Graph y=x^24 y = x2 − 4 y = x 2 4 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 4 x 2 4 Tap for more steps Use the form a x 2 b x c a x 2Now, join the points by a smooth curve The curve so obtained, is the graph of y = x 2 3 x 2 Now, x 2 2 x 4 = 0 ⇒ x 2 3 x 2 − x 2 = 0 ⇒ y = x − 2 ∵ y = x 2 3 x 2 Thus the roots of x 2 2 x 4 = 0 are obtained from the points of intersection of y = x − 2 and y = x 2 3 x 2 Now, form the table for the line y
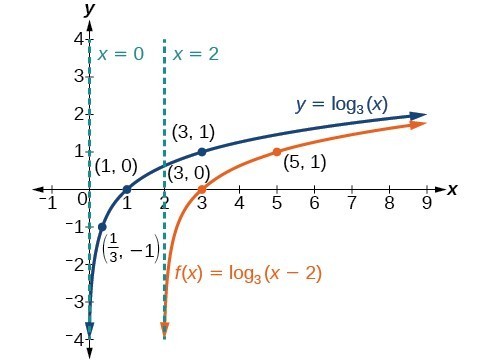



Graphing Transformations Of Logarithmic Functions College Algebra




I F 1 X Or Inverse
x^3x^22x4 = (x1)(x^22x4) = (x1)(x1sqrt(3)i)(x1sqrt(3)i) First note that the sum of the coefficients is zero That is 1124 = 0 So x=1 is a zero and (x1) a factor x^3x^22x4 = (x1)(x^22x4) The remaining quadratic factor is of the form ax^2bxc with a=1, b=2 and c=4 This has discriminant Delta given by the formula Delta = b^24ac = 2^2(4*1*4) =2 (2xy)=2 (xy)4 Simple and best practice solution for 2 (2xy)=2 (xy)4 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itAll equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2xy^ {2}2y3=0 x 2 − 2 x y 2 2 y − 3 = 0 This equation is in standard form ax^ {2}bxc=0




Find Dy Dx Y X 2 1 3 2x 1 Sqrt X 3 4x 1




Algebra Calculator Tutorial Mathpapa
Y=2x3eq 1 y=x2eq 2 so take the value of y from eq 2 and plug it into eq 1 (x2)=2x3 now take x's foundSimple and best practice solution for x^2y^22x4y3=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Two Variable Linear Equations Intro Video Khan Academy




Polynomial Functions
Transcribed Image Textfrom this Question Find the slope of the curve y = x^2 2x 4 at the point P (3, 1) by finding the limit of the secant slopes through point P (b) Find an equation of the tangent line to the curve at P (3, 1)// Plug this in for variable y in equation 2 2 4x 8• (2x4) = 8 2 12x = 24 // Solve equation 2 for the variable x 2 12x = 24 2 x = 2 // By now we know this much x = 2 y = 2x4 z = 3x5y // Use the x value to solve for y y = 2(2)4 = 0 // Use the x and y values to solve for z z = 3Question Y = X3 / 3 X2 / 2 2x 4 1 Find Y' = F'(x) 2 Find Critical Values X= 3 Find Critical Points (x,y) = (x,y) = 4 Find Intervals Of Xvalues Where Function Is Increasing 5 Find Intervals Of Xvalues Where Function Is Decreasing 6 Relative




X A Y B 0 Ax By B2 By Elimination Method Youtube




2x 3y 7 A B 1 X A 2b 2 Y 4 A
Y'*x (3*x^2x*y3*y^2)y* (4*x^2x*y4*y^2)=0 WolframAlpha Rocket science?Algebra Graph y=2 (x3)^24 y = 2(x − 3)2 − 4 y = 2 ( x 3) 2 4 Find the properties of the given parabola Tap for more steps Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 2 a = 2 h = 3 h = 3 k = − 4 k = 4Get stepbystep solutions from expert tutors as fast as 1530 minutes



Quadratics



Math Scene Equations Iii Lesson 3 Quadratic Equations
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




X 2 X 1 4 Sketch The Graph Of Absolute Function Youtube




Vector Analysis By Alimkanwalimtinaa Issuu




Ex 8 1 8 Area Between X Y2 X 4 Is Divided Into Equal




7 Lf X2 Y 2x Y2 And Y 0 Which Of The Following Gauthmath




How To Solve 3 X 2y 5x Y 3 2 X 2 X 2 3y Brainly In




What Is The Equation Of The Tangent To The Curve Y 3x 2 X 1 At Point 1 3 Quora




Solved 72 If F X 2x 4 Which Of The Following Equals Chegg Com




Find Slope Of Tangent Line To Curve 2xy Y 3 4 At 3 2 Youtube




If X X 2 4x 3 2x 4 13 2x 2 5x 9 4x 5 26 8x 2 6x 1 16 X 6 104




Tut1memo




Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6




Solve Squareroot 3x 2 2 For X A 0 B X 1 Chegg Com




Delta Y For The Given Values Of X 1 And X 2 Y 2x Chegg Com



What Are The Asymptotes Of The Curve X 2y 2 X 2 Y 2 2 X 2 Y 2 3 0 Quora




14 2 Limits And Continuity




2x 3y 7 A B X A B Y 3a B 2 Find A B Have An Infinite Number Of Solutions Youtube
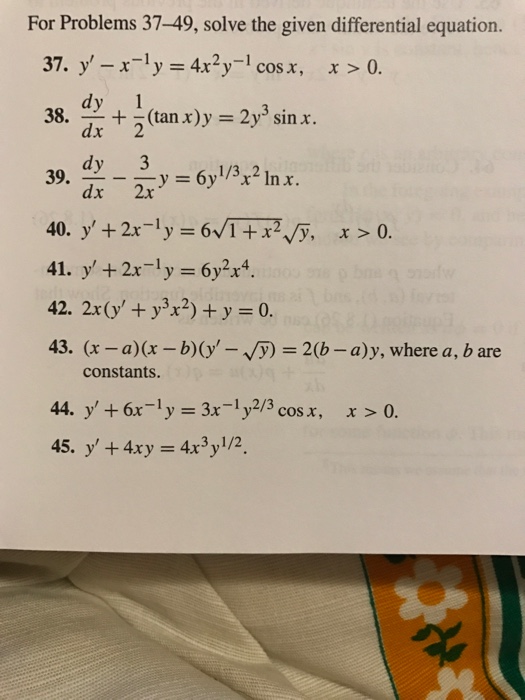



Solve The Given Differential Equation Y X 1 Y Chegg Com



2
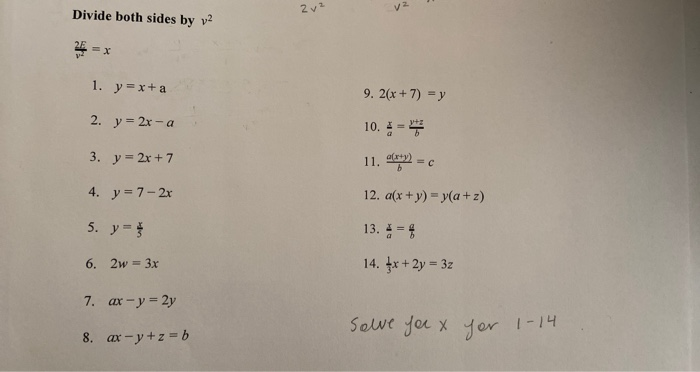



Solved 2v2 V2 Divide Both Sides By V2 1 Y X A 9 2 X Chegg Com




Using Transformations To Graph Functions



2



2




Implicit Differentiation




2 3 Tangent Plane To A Surface Mathematics Libretexts



If 2x Y 23 And 4x Y 19 Then Find The Values Of 5y 2x And Y X 2 Studyrankersonline
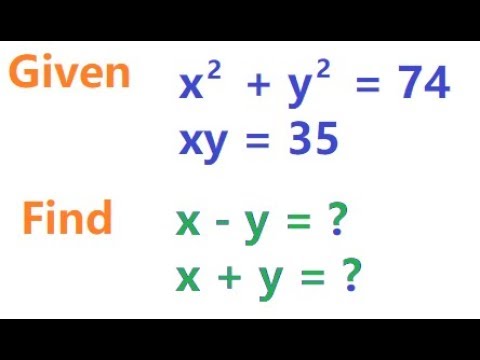



X 2 Y 2 74 And Xy 35 Find X Y And X Y 2x 3y 14 And Xy 8 Find 4x 2 9y 2 Youtube
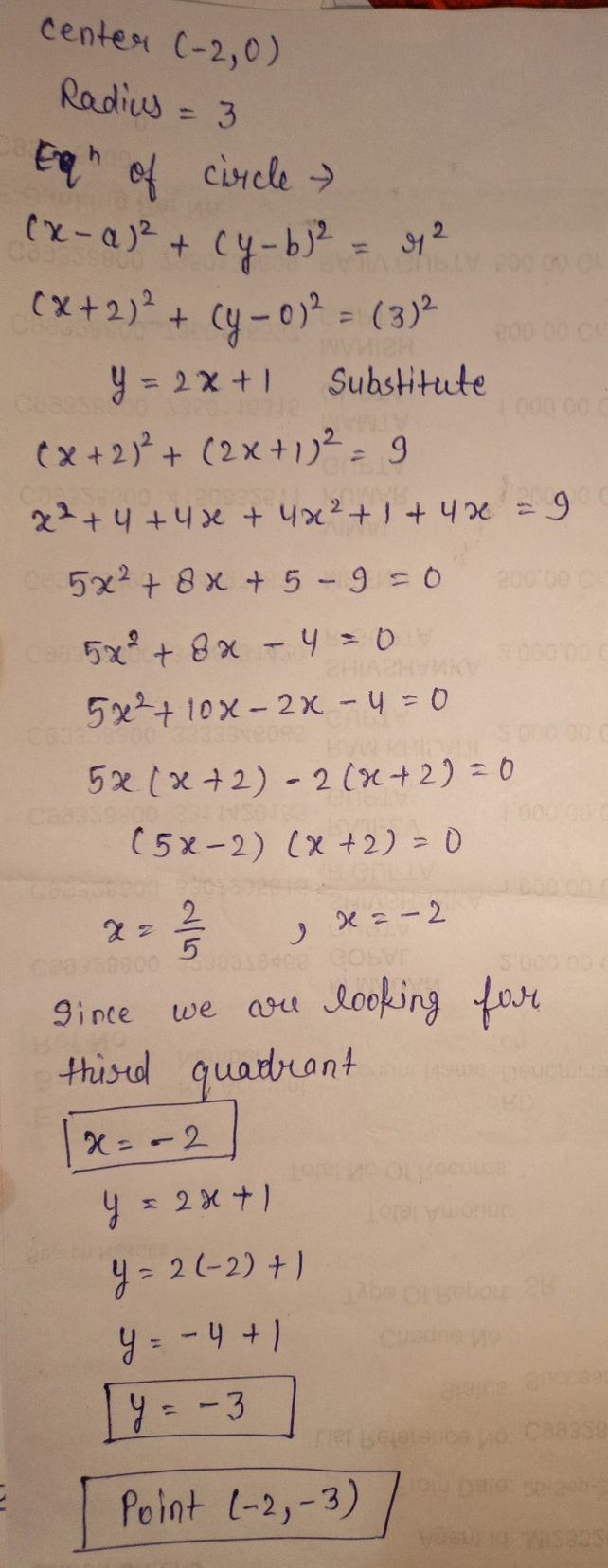



At What Point In The Third Qu See How To Solve It At Qanda



2




1 Functions




The Figure Below Shows F X And Its Local Linearization At X A Y 2x 3 The Local Linearization Is Shown In Blue A What Is The Value Of Al



Quadratics



2



2




The Derivative Function




Warm Up Simplify 5x X A 2b A 2b Multiply Ppt Video Online Download



2



2




What Is The Equation Of The Tangent To The Curve Y 3x 2 X 1 At Point 1 3 Quora



Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline




Y X 2 8x 3 Squareroot X A Y 3 2 X 3 2 Chegg Com




Solve For X And Y Xa Yb 2 Ax By A 2 B 2




X Y A B Ax By A 2 B 2 Solve For X And Y Mathematics Topperlearning Com Vsft4hh



Graphing Types Of Functions



Graphing Quadratic Functions



2




1 Differentiate The Following Functions With Respect To Ww2 Differentiate The Following Functions With Respect To X A Use The Quotient Rule To Differentiate Y 2x 4 3x 4x
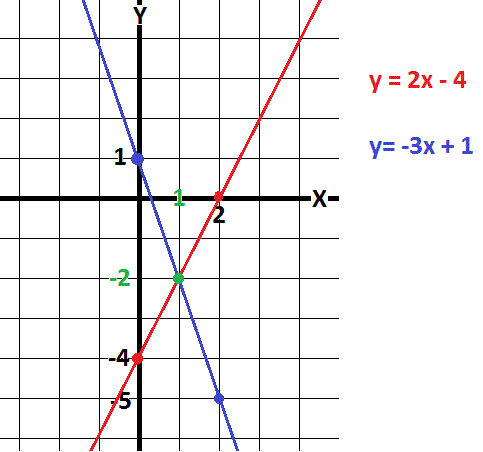



How Do You Solve The System Y 2x 4 And Y 3x 1 By Graphing Socratic



2




Algebra Calculator Tutorial Mathpapa



Asymptotes



2



Graphing Quadratic Functions




Misc 2 Verify Given Function Is A Solution Of Differential



What Are The Asymptotes Of The Curve X 2y 2 X 2 Y 2 2 X 2 Y 2 3 0 Quora
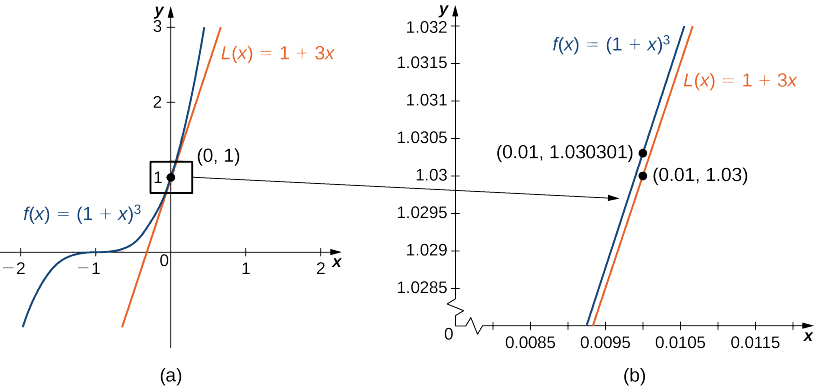



4 2 Linear Approximations And Differentials Mathematics Libretexts




Solve Solve Inequalities With Step By Step Math Problem Solver



Solving Equations Algebraically




Implicit Differentiation



1




Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy




Wolfram Alpha Examples Step By Step Solutions




How Do You Find The Equations Of The Tangent Lines To The Curve Y X 1 X 1 That Are Parallel To The Line X 2y 2 Socratic



1




Solutions Manual For Calculus For Business Economics And The Social A




If X 2 And Y 3 Is The Solution Of The Pair Of Lines 2x 3 Y A And 2 X 3 Y B 2 0 Then Brainly In



Solved Math 111 Home Activity Slope Tangent And Normal Lines Name Course Score Solve The Following Problems 1 Find The Equation Of A L Course Hero




Ex 6 3 15 Find Equation Of Tangent Line To Y X2 2x 7



Graphing Quadratic Functions
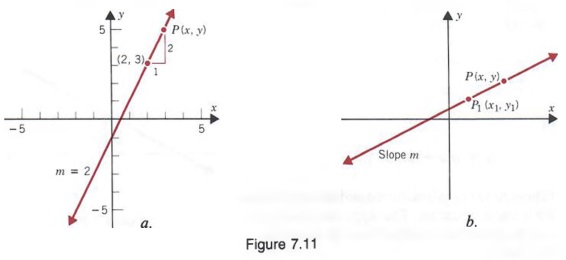



Graph Graph Equations With Step By Step Math Problem Solver
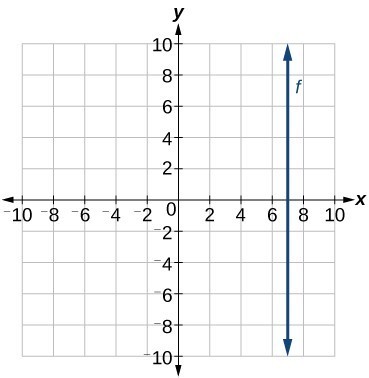



Write The Equation For A Linear Function From The Graph Of A Line College Algebra
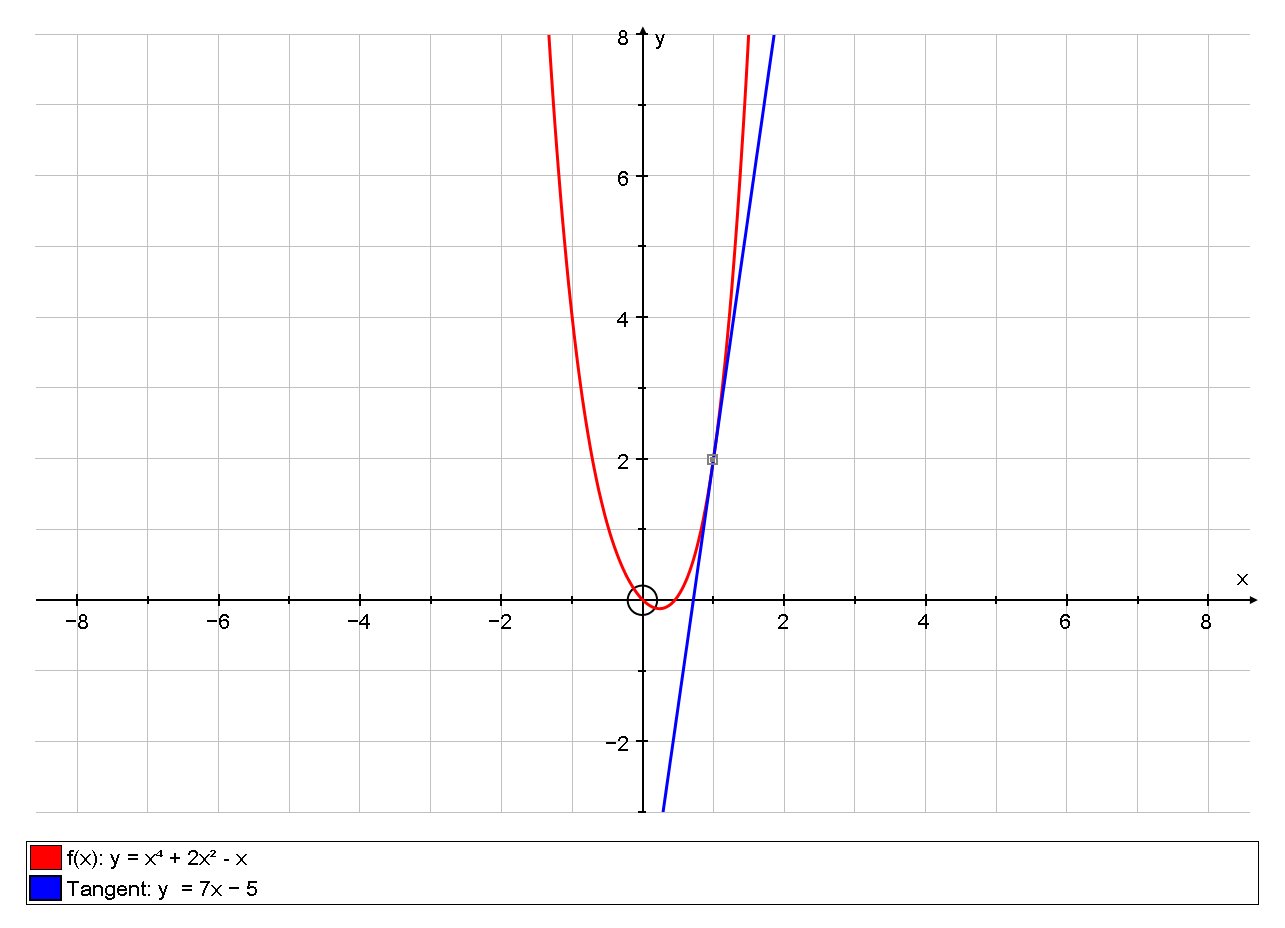



How Do You Find The Equation Of The Tangent Line To The Curve Y X 4 2x 2 X At 1 2 Socratic




Solve System Of Linear Equations Using Matrix Method 2x 3y 3z 5 X 2y Z 4 3x Y 2z 3 Mathematics Shaalaa Com



2




Solutions Manual For College Algebra 10th Edition By Larson Ibsn 9781



Area Of A Region Bounded By Curves




Ml Aggarwal Solutions For Class 10 Maths Chapter 12 Equation Of Straight Line Avail Pdf
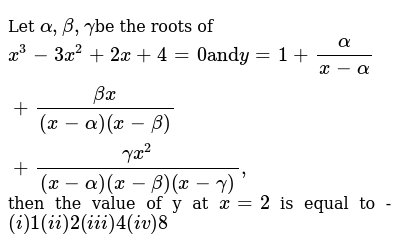



Let Alpha Beta Gammabe The Roots Of X 3 3x 2 2x 4 0 And Y 1 Al



Volume Of A Solid Of Revolution Disks And Washers


